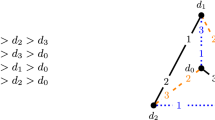Abstract
We study popular matchings in the many-to-many matching problem, which is given by a graph \(G = (V,E)\) and, for every agent \(u\in V\), a capacity \(\textsf {cap}(u) \ge 1\) and a preference list strictly ranking her neighbors. A matching in G is popular if it weakly beats every matching in a majority vote when agents cast votes for one matching versus the other according to their preferences. First, we show that when \(G = (A\cup B,E)\) is bipartite, e.g., when matching students to courses, every pairwise stable matching is popular. In particular, popular matchings are guaranteed to exist. Our main contribution is to show that a max-size popular matching in G can be computed in linear time by the 2-level Gale–Shapley algorithm, which is an extension of the classical Gale–Shapley algorithm. We prove its correctness via linear programming. Second, we consider the problem of computing a max-size popular matching in \(G = (V,E)\) (not necessarily bipartite) when every agent has capacity 1, e.g., when matching students to dorm rooms. We show that even when G admits a stable matching, this problem is \(\mathsf {NP}\)-hard, which is in contrast to the tractability result in bipartite graphs.



Similar content being viewed by others
Notes
\(M_0\) is a maximal element of a relation \(\succsim \) if for all elements \(M_1\) we have: \(M_1\succsim M_0\) implies \(M_0\sim M_1\).
References
Abraham, D.J., Irving, R.W., Kavitha, T., Mehlhorn, K.: Popular matchings. SIAM J. Comput. 37(4), 1030–1045 (2007)
Askalidis, G., Immorlica, N., Kwanashie, A., Manlove, D., Pountourakis, E.: Socially Stable matchings in the hospitals/residents problem. In: the 13th International Symposium on Algorithms and Data Structures (WADS), pp. 85–96 (2013)
Blair, C.: The lattice structure of the set of stable matchings with multiple partners. Math. Oper. Res. 13, 619–628 (1988)
Biro, P., Irving, R.W., Manlove, D.F.: Popular matchings in the marriage and roommates problems. In: the 7th International Conference in Algorithms and Complexity (CIAC), pp. 97–108 (2010)
Brandl, F., Kavitha, T.: Popular matchings with multiple partners. In: the 37th Foundations of Software Technology and Theoretical Computer Science (FSTTCS) (2017)
Canadian Resident Matching Service. How the matching algorithm works. Web document available at http://carms.ca/algorithm.htm
Condorcet, J.A.N.C.: Essai sur l’application de l’analyse à la probabilité des décisions rendues à la pluralité des voix. Imprimerie Royale, Paris (1785)
Cseh, Á.: Popular matchings. In: Trends in Computational Social Choice, Edited by Ulle Endriss, COST (European Cooperation in Science and Technology), pp. 105–122 (2017)
Cseh, Á., Huang, C.-C., Kavitha, T.: Popular matchings with two-sided preferences and one-sided ties. In: the 42nd International Colloquium on Automata, Languages, and Programming (ICALP): Part I, pp. 367–379 (2015)
Cseh, Á., Kavitha, T.: Popular edges and dominant matchings. In: the 18th International Conference on Integer Programming and Combinatorial Optimization (IPCO), pp. 138–151 (2016)
Faenza, Y., Kavitha, T., Powers, V., Zhang, X.: Popular matchings and limits to tractability. In: The Conference is the 30th Annual ACM-SIAM Symposium on Discrete Algorithms, SODA 2019, pp. 2790–2809 (2019)
Gale, D., Shapley, L.S.: College admissions and the stability of marriage. Am. Math. Month. 69(1), 9–15 (1962)
Gale, D., Sotomayor, M.: Some remarks on the stable matching problem. Discrete Appl. Math. 11(3), 223–232 (1985)
Gärdenfors, P.: Match making: assignments based on bilateral preferences. Behav. Sci. 20(3), 166–173 (1975)
Gupta, S., Misra, P., Saurabh, S., Zehavi, M.: Popular matching in roommates setting is NP-hard. The Conference is the 30th Annual ACM-SIAM Symposium on Discrete Algorithms, SODA 2019, pp. 2810–2822 (2019)
Gusfield, D., Irving, R.W.: The Stable Marriage Problem: Structure and Algorithms. MIT Press, Boston (1989)
Hamada, K., Iwama, K., Miyazaki, S.: The hospitals/residents problem with lower quotas. Algorithmica 74(1), 440–465 (2016)
Hirakawa, M., Yamauchi, Y., Kijima, S., Yamashita, M.: On the structure of popular matchings in the stable marriage problem—who can join a popular matching? In: The 3rd International Workshop on Matching Under Preferences (MATCH-UP) (2015)
Huang, C.-C.: Classified stable matching. In: the 21st Annual ACM-SIAM Symposium on Discrete Algorithms (SODA), pp. 1235–1253 (2010)
Huang, C.-C., Kavitha, T.: Popular matchings in the stable marriage problem. Inf. Comput. 222, 180–194 (2013)
Huang, C.-C., Kavitha, T.: Popularity, self-duality, and mixed matchings. In: the 28th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA), pp. 2294–2310 (2017)
Irving, R.W.: An efficient algorithm for the stable roommates problem. J. Algorithms 6, 577–595 (1985)
Irving, R.W., Manlove, D.F., Scott, S.: The hospitals/residents problem with ties. In: the 7th Scandinavian Workshop on Algorithm Theory (SWAT), pp. 259–271 (2000)
Irving, R.W., Manlove, D.F., Scott, S.: Strong stability in the hospitals/residents problem. In the 20th Annual Symposium on Theoretical Aspects of Computer Science (STACS), pp. 439–450 (2003)
Kavitha, T.: A size-popularity tradeoff in the stable marriage problem. SIAM J. Comput. 43(1), 52–71 (2014)
Kavitha, T.: Popular half-integral matchings. In: the 43rd International Colloquium on Automata, Languages, and Programming (ICALP), pp. 22.1–22.13 (2016)
Kavitha, T.: Max-size popular matchings and extensions. http://arxiv.org/pdf/1802.07440.pdf
Kavitha, T., Mestre, J., Nasre, M.: Popular mixed matchings. Theor. Comput. Sci. 412(24), 2679–2690 (2011)
Király, T., Mészáros-Karkus, Zs: Finding strongly popular b-matchings in bipartite graphs. Electron. Notes Discrete Math. 61, 735–741 (2017)
Manlove, D.F.: Algorithmics of Matching Under Preferences. World Scientific Publishing Company Incorporated, Singapore (2013)
Manlove, D.F.: The Hospitals/Residents Problem. Encyclopedia of Algorithms, pp. 926–930. Springer, Berlin (2015)
Nasre, M., Rawat, A.: Popularity in the generalized hospital residents setting. In: the 12th International Computer Science Symposium in Russia (CSR), pp. 245–259 (2017)
National Resident Matching Program. Why the Match? Web document available at http://www.nrmp.org/whythematch.pdf
Roth, A.E.: The evolution of the labor market for medical interns and residents: a case study in game theory. J. Polit. Econ. 92(6), 991–1016 (1984)
Roth, A.E.: Stability and polarization of interest in job matching. Econometrica 53, 47–57 (1984)
Roth, A.E.: On the allocation of residents to rural hospitals: a general property of two-sided matching markets. Econometrica 54(2), 425–427 (1986)
Sotomayor, M.: Three remarks on the many-to-many stable matching problem. Math. Soc. Sci. 38, 55–70 (1999)
Subramanian, A.: A new approach to stable matching problems. SIAM J. Comput. 23(4), 671–700 (1994)
Teo, C.-P., Sethuraman, J.: The geometry of fractional stable matchings and its applications. Math. Oper. Res. 23(4), 874–891 (1998)
Acknowledgements
We thank the reviewers for their helpful comments. The first author wishes to thank Larry Samuelson for comments on the motivation for popular matchings. The second author wishes to thank David Manlove and Bruno Escoffier for asking her about popular matchings in the hospitals/residents setting.
Author information
Authors and Affiliations
Corresponding author
Appendix: An Interesting Example
Appendix: An Interesting Example
Given a many-to-many matching instance \(G = (A \cup B,E)\), we investigate the possibility of constructing a corresponding one-to-one matching instance \(G' = (A'\cup B',E')\) (with strict preference lists) in order to show a reduction from the max-size popular matching problem in G to one in \(G'\). The vertex set \(A'\) will have \(\textsf {cap}(a)\) many copies \(a_1, a_2, \ldots \) of every \(a \in A\) and \(B'\) will have \(\textsf {cap}(b)\) many copies \(b_1, b_2, \ldots \) of every \(b \in B\). The edge set \(E'\) has \(\textsf {cap}(a)\cdot \textsf {cap}(b)\) many copies of edge (a, b) in E. If \(v \succ _u v'\) in G then we have \(v_i \succ _{u_k} v'_j\) for each \(i \in \{1,\ldots ,\textsf {cap}(v)\}\), \(j \in \{1,\ldots ,\textsf {cap}(v')\}\), and \(k \in \{1,\ldots ,\textsf {cap}(u)\}\). Among the copies \(v_1,\ldots ,v_{\textsf {cap}(v)}\) of the same vertex v, we will set \(v_1 \succ _{u_k} \cdots \succ _{u_k} v_{\textsf {cap}(v)}\), for each vertex \(u_k\) in \(G'\).
Given any matching \(\tilde{M}\) in \(G'\), we define \(\textsf {proj}(\tilde{M})\) as the projection of \(\tilde{M}\), which is the matching obtained by dropping the subscripts of all vertices. Observe that \(\textsf {proj}(\tilde{M})\) obeys all capacity bounds in G. We will now consider the many-to-one or the hospitals/residents setting: so there are no multi-edges in \(\textsf {proj}(\tilde{M})\). It would be interesting to be able to show that every popular matching M in G has a realization\(\tilde{M}\) in \(G'\) (i.e., \(\textsf {proj}(\tilde{M}) = M\)) such that \(\tilde{M}\) is a popular matching in \(G'\).
However the above statement is not true as shown by the following example. Let \(G = (R \cup H, E)\) where \(R = \{p,q,r,s\}\) and \(H = \{h,h',h''\}\) where \(\textsf {cap}(h) = 2\) and \(\textsf {cap}(u) = 1\) for all other vertices u. The preference lists are as follows:

Consider the matching \(N = \{(p,h),(q,h'),(r,h)\}\). Claim 2 below shows that N is a popular matching. Our proof of popularity of N will use the sufficient condition for popularity shown in Theorem 1 and follows the approach used in Theorem 2.
Claim 2
The matching N is popular in G.
The edges of the matching \(N'\) are bold and the non-matching edges in \(G'_N\) are dashed. For simplicity, we have not included self-loops here. Note that the edge \((q_1,h_2)\) is a blocking edge to \(N'\) as both \(q_1\) and \(h_2\) prefer each other to their respective partners in \(N'\), i.e., \(\textsf {wt}_{N}(q_1,h_2) = 2\) and \(\textsf {wt}_{N}(e) = 0\) for all other edges e in \(G'_N\)
Proof
We will use the notation introduced at the beginning of Sect. 3. So we have \(R' = \{p_1,q_1,r_1,s_1\}\) and \(H' = \{h_1,h_2,h'_1,h''_1\}\). Let \(N' = \{(p_1,h_1),(q_1,h'_1),(r_1,h_2)\}\) (see Fig. 4).
We need to show that every perfect matching in the weighted graph \(G'_N\) has weight at most 0. We will show this by constructing a witness or a solution to the dual LP corresponding to the primal LP which is the max-weight perfect matching problem in \(G'_N\). This solution is the following: \(\alpha _{p_1} = \alpha _{h_1} = \alpha _{s_1} = \alpha _{h''_1} = 0\) while \(\alpha _{q_1} = \alpha _{h_2} = 1\) and \(\alpha _{r_1} = \alpha _{h'_1} = -1\). The above solution is dual-feasible since every edge in \(G'_N\) is covered by the sum of \(\alpha \)-values of its endpoints; in particular, note that \(\alpha _{q_1} + \alpha _{h_2} = 2 = \textsf {wt}_{N}(q_1,h_2)\). The dual optimal solution is at most \(\sum _{u \in R' \cup H'}\alpha _u = 0\). So the primal optimal solution is also at most 0, in other words, N is a popular matching in G. \(\square \)
Note that the graph \(G'\) has two extra edges relative to \(G'_N\): these are \((p_1,h_2)\) and \((r_1,h_1)\). With respect to realizations of N in \(G'\), there are 2 candidates: these are \(N_1 = \{(p_1,h_1),(q_1,h'_1),(r_1,h_2)\}\) and \(N_2 = \{(p_1,h_2),(q_1,h'_1),(r_1,h_1)\}\).
Claim 3
Neither \(N_1\) nor \(N_2\) is popular in \(G'\).
Proof
Consider the matching \(M_1 = \{(p_1,h''_1),(q_1,h_2),(r_1,h_1)\}\). The vertices \(p_1\), \(h_1\), and \(h'_1\) prefer \(N_1\) to \(M_1\) while the vertices \(q_1\), \(h_2\), \(r_1\), and \(h''_1\) prefer \(M_1\) to \(N_1\) and \(s_1\) is indifferent. Thus \(M_1\) is more popular than \(N_1\), i.e., \(N_1\) is not a popular matching in \(G'\).
Consider the matching \(M_2 = \{(p_1,h_1),(q_1,h'_1),(s_1,h_2)\}\). The vertices \(r_1\) and \(h_2\) prefer \(N_2\) to \(M_2\) while the vertices \(p_1\), \(h_1\), and \(s_1\) prefer \(M_2\) to \(N_2\) and \(q_1\), \(h'_1\), and \(h''_1\) are indifferent. Thus \(M_2\) is more popular than \(N_2\), i.e., \(N_2\) is not a popular matching in \(G'\). Hence neither \(N_1\) nor \(N_2\) is popular in \(G'\). \(\square \)
Note that the above instance can easily be transformed to another instance G with a max-size popular matching that cannot be realized as a popular matching in \(G'\). In fact, it is easy to show that every popular matching in \(G'\) gets projected to a popular matching in G. However as illustrated by the example above, there may exist popular matchings in G that cannot be realized as popular matchings in \(G'\).
Rights and permissions
About this article
Cite this article
Brandl, F., Kavitha, T. Two Problems in Max-Size Popular Matchings. Algorithmica 81, 2738–2764 (2019). https://doi.org/10.1007/s00453-019-00553-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00453-019-00553-0