Skip to main content
SpringerLink
Log in

Fragility curves for steel–concrete composite shear wall building with torsional irregularity

  • Original Paper
  • Published:
Asian Journal of Civil Engineering Aims and scope Submit manuscript

Abstract

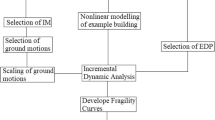
In this study, building model which is trapezoidal in plan with steel–concrete composite shear walls (SCCMSWs) is reduced to 1/4th scale in order to validate modal information and joint responses analytical results with AZALEE shake table under the scope of the SMART program. Incremental dynamic analysis (IDA) is performed on numerical model, and the maximum inter-storey drift is determined as a response parameter for all simulations. Fourteen real ground motion records are used to study the ground motion variability. Further, seismic fragility curves are developed based on IDA results to assess uncertainties in hazard evaluation of structure. Damage probability matrices under various damage states obtained from fragility curves are compared for building as per pre-established damage indicators of SMART 2008 and HAZUS 2003 specifications. It is concluded that, SCCMSWs building structure considered in the study behaves well when subjected to severe earthquakes.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Abbreviations

P (≤ D):

Probability that a ground motion with intensity measure (IM = xi) will cause the structure to collapse

Ø():

Standard normal cumulative distribution function (CDF)

λ :

Mean of natural logarithmic of IM

ξ :

Standard deviation of natural logarithmic of IM (also referred to as the dispersion of IM)

ϕ y :

Yield curvature

L v :

Shear length constant for symmetrical elements (1/2 of the total element length L)

H :

Total section height

d b :

Mean diameter of the longitudinal bars in the affected section

f y :

Yield strength of the longitudinal reinforcement steel [MPa]

f c :

Concrete compression strength [MPa]

a v :

av = 1 if shear cracking is expected to precede flexural yielding at the end section; otherwise av=0

z :

Length of internal lever arm, taken equal to dr–d′ in beams, columns, or walls with barbelled or T-section, or to 0.8 h in walls with rectangular section [mm]

d r :

Depth to the tension reinforcement [mm]

d′ :

Depth to the compression reinforcement [mm]

ϕ u :

Ultimate curvature

L p :

Plastic hinge length [mm]

V cm :

Shear capacity of steel shape in the composite member

V rc :

Shear capacity of the RC portion in the composite member

V s :

Shear capacity of the reinforcement in the composite member

A ws :

Area of steel web of encased steel section

b s :

Section width

d s :

Effective depth

f ′c :

Unconfined compressive strength

N u :

Axial load on the section

A g :

Concrete area

A s :

Area of transverse reinforcement

f s :

Yield strength of transverse reinforcement

S :

Spacing of transverse reinforcement

References

  • ACI 318. (2008). Building code requirements for structural concrete and commentary. Detroit: American Concrete Institute.

  • Akansel, V.H., Yakut, A., & Gülkan P. (2012). Fragility of shear wall buildings with torsional irregularity. 15th World Conference on Earthquake Engineering, Lisboa.

  • ASCE/SEI 41-06. (2007). Seismic rehabilitation of existing buildings. American Society of Civil Engineers.

  • ATC-40. (1996). Seismic evaluation and retrofit of concrete buildings (vol-1). Applied Technology Council, Redwood City, California.

  • Cinitha, A., Umesha, P.K., & Iyer N.R. (2012). Nonlinear static analysis to assess performance and vulnerability of code-conforming RC Buildings. WSEAS Transactions on App lied and Theoretical Mechanics 7(1).

  • Crijanovschi, S., Richard, B., Chaudat, T., & Atanasiu, G.M. (2012). Preliminary numerical analysis of a reinforced concrete mock up: effects of thermal breakers and shaking table. 15th World Conference on Earthquake Engineering, Lisboa.

  • Dan, D., Fabin, A., & Stoian, V. (2011). Theoretical and experimental study on composite steel-concrete shear wall with vertical steel encased profiles. Journal of Constructional Steel Research, Elsevier. https://doi.org/10.1016/j.jcsr.2010.12.013.

    Google Scholar 

  • Fabian, A., Daniel, D., Stoian, V., Demeter, I., Nagy-Gyorgy, T., & Floruţ, C. (2011). Comparative study concerning the seismic behavior of composite steel–concrete structure steel encased profiles. Proceedings Fib Symposium PRAGUE, Session 5-6: Composites and Hybrids, pp. 01-06.

  • Fahjan, Y.M., Doran B., Akbs B., & Kubin, J. (2012). Pushover Analysis for Performance Based-Seismic Design of RC Frames with Shear Walls. 15 th World Conference on Earthquake Engineering, Lisboa.

  • Fahjan, Y.M., Kubin, J., & Tan, M.T. (2010). Non-linear analysis methods for RC buildings with shear walls. 14th European Conference on Earthquake Engineering.

  • FEMA 356. (2000). Prestandard and commentary for seismic rehabilitation of buildings. Applied Technology Council for the Building Seismic Safety Council, Washington, DC.

  • FEMA P695. (2009). Quantification of building seismic performance. Applied Technology Council, California.

  • Gaikwad, P.S., & Tolani, K. (2015). Review paper on dynamic analysis of buildings. International Journal of Current Engineering and Technology, 5(2).

  • IS 1893. (2016). Indian standard, criteria for earthquake resistant design of structures (part 1), general provisions and buildings. (Sixth Revision), Bureau of Indian Standards, New Delhi, India.

  • Lermitte, S. J., Chaudat, T., & Courtois, A. (2009). SMART2008 Project experimental tests of a reinforced concrete buildings subjected to torsion. 20th International Conference on Structural Mechanics in Reactor Technology (SMiRT 20–Div. V), Espoo, Finland.

  • Luco, N., & Cornell, C. A. (2002). Structure-specific, scalar intensity measures for near-source and ordinary earthquake ground motions. Earthquake Spectra, 23(2), 357–392. https://doi.org/10.1193/1.2723158.

    Article  Google Scholar 

  • Mander, J. B., Priestley, M. J., & Park, R. (1988a). Observed stress–strain behavior of confined concrete. ASCE Journal of Structural Engineering, 114(8), 1827–1849.

    Article  Google Scholar 

  • Mander, J. B., Priestley, M. J. N., & Park, R. (1988b). Theoretical stress–strain model of confined concrete. ASCE Journal of Structural Engineering, 114(8), 1804–1826.

    Article  Google Scholar 

  • Mieses, L.A., Lopez, R.R., & Saffar, A. (2007). Development of fragility curves for medium-rise RC shear wall residential buildings in Puerto Rico. Association Argentina de Mecania Computational, 2712–2727.

  • Nazirzadeh, S., Akansel, V.H., & Yakut, A. (2012). Numerical simulation of shaking table test of a RC shear wall structure with torsional irregularity. 15th World Conference on Earthquake Engineering, Lisboa

  • EC-8, Part 3. (1994–2003). European Committee for Standardization. Design Provisions for Earthquake Resistance of Structures. Brussels.

  • Patil, V.S., & Tande, S.N. (2018). Probabilistic verses Deterministic Method of Seismic Performance evaluation. Asian Journal of Civil Engineering, Springer International publishing AG., Part of Springer Nature, http://doi.org/10.1007/s42107-018-0015-6.

  • Phadnis, P. P., Kulkarni, D. K., Kulkarni, A. B., & Karjinni, V. V. (2018). Performance of composite steel-concrete shear walls with encased vertical steel sections. The Indian Concrete Journal, 92(7), 74–81.

    Google Scholar 

  • Raju, R. K., Cinitha, A., & Iyer, N. R. (2012). Seismic performance evaluation of existing RC buildings designed as per past code of practice. Indian Academy of Sciences, 37(Part 2), 281–297.

    Google Scholar 

  • Shakib H., & Pirizadeh, M. (2014). Probabilistic seismic performance assessment of setback buildings under bidirectional excitation. Journal of Structural Engineering, 140(2).

  • Shome, N., & Cornell, C.A. (1999). Probabilistic seismic demand analysis of nonlinear structures. Report no. RMS-35, Department of Civil and Environmental Engineering, Standford University, Standford, California.

  • Shome, N., & Cornell, C.A. (2000). Structural seismic demand analysis: Consideration of collapse. Proceedings of the 8th ASCE Specialty Conference on Probabilistic Mechanics and Structural Reliability, Paper No. 119, Norte Dame, pp. 1–6.

  • SMART 2008 Project: Seismic Design and Best-estimate Methods Assessment for Reinforced Concrete Buildings Subjected to Torsion and Non-linear Effects Earthquake Blind Prediction Contest and Fragility Assessment

  • Stoian, V., Dan, D., & Fabian, A. (2011). Composite shear walls with encased profiles. New solution for buildings placed in seismic area. Acta Technica Napocensis Civil Engineering and Architecture, 54, 5–12.

    Google Scholar 

  • HAZUS®MH 2.1, Technical manual. (2003). Multi-hazard loss estimation methodology earthquake model. Federal Emergency Management Agency, Washington, D.C., United States

  • Vamvatsikos, D., & Cornell, C.A. (2002a). Incremental dynamic analysis. Earthquake Engineering and Structural Dynamics, 491–514.

  • Vamvatsikos, D., & Cornell, C.A. (2002b). The Incremental Dynamic Analysis and It’s Application to Performance-Based Earthquake Engineering. 12th European Conference on Earthquake Engineering. Paper ref. 479.

  • Verudo, C.M., Hube, M.A., Favier, P., & Saitua, F. (2017). Analytical fragility curves of high-rise reinforced concrete shear wall buildings. 16th World Conference on Earthquake Engineering (pp. 1–11).

  • Wen, Y.K., Ellingwood, B.R., & Bracci, J. (2004). Vulnerability function framework for consequence-based engineering, vol. DS-4, MAE Center Project, DS-4 Report.

  • Weng, C. C., Yen, S. I., & Chen, C. C. (2001). Shear strength of concrete-encased composite structural members. Journal of Structural Engineering, 127(10), 1190–1197. (Paper No. 18653).

    Article  Google Scholar 

  • Zhao, Q., & Astanesh-Asl, A. (2007). Seismic behavior of composite shear wall systems and its application of smart structures technology. Steel Structures, 7, 69–75.

    Google Scholar 

  • PEER (Pacific Earthquake Engineering Research Center), NGA Database-http://peer.berkeley.edu/peer_ground_motion_database.

Download references

Author information

Authors and Affiliations

  1. Department of Technology, Shivaji University, Kolhapur, 416004, Maharashtra, India

    P. P. Phadnis

  2. Kolhapur Institute of Technology’s College of Engineering (Shivaji University), Kolhapur, 416234, Maharashtra, India

    V. V. Karjinni

Authors
  1. P. P. Phadnis
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. V. V. Karjinni
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to P. P. Phadnis.

Ethics declarations

Conflict of interest

On behalf of all authors, I (corresponding author) declare that there is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Phadnis, P.P., Karjinni, V.V. Fragility curves for steel–concrete composite shear wall building with torsional irregularity. Asian J Civ Eng 20, 1163–1178 (2019). https://doi.org/10.1007/s42107-019-00174-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42107-019-00174-6

Keywords

Search

Navigation