Comparison of data processing algorithm performance for optical and conductivity void probes

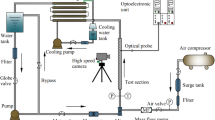
Abstract

In commercial nuclear reactors, heat exchangers, and bubble column reactors, two-phase flows are present. When predicting the safety and process efficiency of these systems, it is necessary to model the behavior found in them. The most common model used in two-phase flows is the two-fluid model due to its practicality. In the two-fluid model, two key parameters are the void fraction (VF, also known as the gas fraction or gas holdup) and interfacial area concentration (IAC, also known as interfacial area density). In order to produce accurate results, the bubbles are separated into groups based on the transport properties. When benchmarking models, experimental data are required. In many cases the experimental data are produced with the use of intrusive conductivity or optical probes. Recently a new data processing algorithm was developed to improve bubble interface identification and implement a method to group bubbles based on diameter rather than chord length. In this paper, the new data processing algorithm is evaluated by comparing the results when using both conductivity and optical probes. At a data acquisition frequency of 22 kHz, the optical probe collected more bubbles than the conductivity probe using the old algorithm. The new algorithm results in similar bubble counts for both instruments. There is a shift in bubbles from Group 1 to Group 2 in both the optical and conductivity probes. The new bubble size calculation means that several bubbles, which were previously classified as “spherical/distorted”, are now classified as “cap/slug/churn” bubbles for both the optical and conductivity probes. However due to low sample rates used in this research, the IAC is larger for the conductivity probe when compared to the optical probe by 10% to 60%. While some of these changes were expected, the increase in the IAC was larger than the reported uncertainty of the instruments.