1 Introduction

Seismic risk analyses have traditionally been built upon existing tools developed for the purposes of evaluating seismic hazard. These seismic hazard analyses are always conducted for a single spatial location and have traditionally made use of the ergodic assumption (Anderson and Brune 1999), with exceptions being limited to high-level applications for critical facilities such as nuclear power plants, e.g., Rodriguez-Marek et al. (2014).

For regional, or large-portfolio, risk analyses, ground-motion demands need to be prescribed at multiple spatial locations simultaneously, and these spatial locations often represent broader spatial regions around those locations within the analysis framework. Issues associated with the discretisation of ground-motion fields and exposure distributions are often over-looked. In particular, ground motion fields are developed using statistical properties between individual points, rather than between spatial regions (Stafford 2012).

The ergodic assumption, in the context of ground-motion modelling, is the assumption that the statistical properties of ground-motions at one particular location can be represented by pooling data from many different spatial locations with nominally similar characteristics. This assumption is necessary because individual sites have insufficient numbers of ground-motion recordings to permit robust site-specific ground-motion models to be developed. As the data comes from nominally similar spatial locations, the actual differences from site-to-site and region-to-region that remain within the data has impacts upon both the median predictions of ground-motion models and the associated variability derived from the data.

The application of the ergodic assumption therefore enables large databases of empirical observations to be compiled, and for robust ground-motion models to then be derived. However, the associated cost is that the derived ergodic ground-motion model is calibrated to this ergodic database rather than to the target site, and to the most relevant rupture scenarios that drive the hazard and risk at this site. Recent efforts (Kuehn et al. 2016; Landwehr et al. 2016; Stafford 2014; Stafford 2019) have looked to develop ground-motion models that make use of ergodic databases, but still allow for site- or region-specific features to be accounted for within partially non-ergodic frameworks. An aspect of non-ergodic ground-motion modelling that has received limited attention thus far is the impact that relaxing the assumption has upon correlation models that are required within risk analyses.

The present chapter focusses upon aspects of these two issues: impacts of spatial discretisation upon correlation models; and, non-ergodic ground-motion modelling issues, with a particular focus upon spatial correlation and aftershock sequences. The following section, Sect. 8.2, discusses the impacts of discretisation upon correlations that are required within risk analyses. Thereafter, Sect. 8.3 discusses the impacts of non-ergodic ground-motion models upon spatial correlations. Section 8.4 then looks at how non-ergodic concepts can be used to refine aftershock risk analyses, before the chapter closes with some high-level conclusions.

2 Correlations Among Intensity Measures

Models that have been published to represent correlations among intensity measures fall into two broad classes: those that represent correlations between two different intensity measures at a single spatial location, e.g., Baker and Bradley (2017); Baker and Jayaram (2008), and those that represent the spatial location of two intensity measures (potentially the same intensity measure) at two different spatial locations, e.g., Foulser Piggott and Stafford (2012); Jayaram and Baker (2009). These models are all derived on the basis of point observations of intensity measure fields because recording instruments at themselves located at particular points in space.

However, within portfolio risk analyses it is not usually feasible to perform calculations for each structure within the portfolio. Rather, buildings are grouped into a set of structural classes that have different representative structural characteristics, and intensity measures are computed at distinct locations that actually represent discrete spatial regions. Ideally, the results of a risk analysis that one obtained from considering every building within the portfolio should be the same (or, on average, very similar) to that obtained from working with discrete building classes and spatially-discretised fields of intensity measures. The only way that this ideal scenario can be achieved is if a great deal of care is taken to ensure the appropriate mapping between correlations and covariances between points and those over spatial regions. Previous attempts to look at the influence of spatial discretisation upon risk results (Bal et al. 2010) have not appropriately dealt with the relation between point-to-point spatial correlations and region-to-region correlations.

The types of correlations that may need to be considered within a regional risk analysis are shown schematically in Fig. 8.1. In this figure, ground-motions are computed at the white nodal locations within each grey cell. These cells can contain multiple structures. The leftmost panel shows a case where we have buildings from the same class present within a single cell. Given that all of these buildings have the same fragility curves, requiring the same intensity measure as an input, and that this intensity measure is only predicted at a single location within the cell, the demands upon all buildings within the cell are treated as being identical. Clearly, that modelling representation is not consistent with reality, and the quality of the assumption degrades as the spatial resolution reduces.

Fig. 8.1
figure 1

Correlation cases to consider in portfolio risk analyses. Common assumptions about the correlations made in each case are annotated above and below each panel

Full size image

To enable our risk results to scale appropriately for different spatial correlations we need to account for the spatial differences in building locations within a given cell. This is true for all cases shown in Fig. 8.1 and influences the effective correlations that we use for buildings of the same class, and of different classes. When also considering spatial correlations across different cells we also need to account for the different site-to-site distances that can arise across those two cells.

To explain these issues more formally, the next section introduces how correlations between two points are traditionally handled, and then explains what the impact of spatial discretisation is for these models.

2.1 Point-Wise Correlations

Figure 8.1 showed that we need to have general correlation models that describe correlations between two buildings, characterised by response periods Ti and TjFootnote 1, and located at sites xp and xq, respectively. That is, we need to define the correlation between the intensity measures ln Sa({Ti, xp}) and ln Sa({Tj, xq}).

Although more elaborate approaches are also available (Loth and Baker 2013), the conventional way to represent this correlation is to combine inter-period correlation models (Baker and Bradley 2017; Baker and Jayaram 2008) with spatial correlation models at a given period (Jayaram and Baker 2009). This Markovian approximation (Goda and Hong 2008) is represented in Eq. 8.1

$$\rho \left( \left\{ T_{i}, {\bf x}_{p} \right\},\left\{ T_{j}, {\bf x}_{q} \right\} \right) \approx \rho \left( T_{i}, T_{j} \right) \times \rho \left( {{\bf x}_{p}, {\bf x}_{q}} | \max\left(T_{i}, T_{j} \right) \right)$$
(8.1)

This approach is conventionally adopted within portfolio risk analyses. Buildings are assigned to discrete building classes, and each class has a fragility curve developed for it that utilises at least one intensity measure as an input. The risk analysis framework uses Monte Carlo simulation to generate spatially-correlated ground-motion fields at individual co-ordinates, and the motions at these coordinates are input to fragility curves to establish the demands for all buildings in each class.

2.2 Effects of Spatial Discretization

Consider again the leftmost panel of Fig. 8.1 in which we have multiple buildings of the same class located within a single cell. In reality, each building occupies a different spatial position and will receive its own value of spectral acceleration. These acceleration values will be correlated spatially over the cell because there will be commonalities associated with source amplitudes, wave propagation paths, and site conditions. The particular amplitude experienced by each building depends upon the particular realisation of the random field as well as its actual location within the cell. As spatial correlation models show decreasing correlation with increasing separation distance (Jayaram and Baker 2009), the further a building is located from the point within the cell where the ground-motion field is defined, the weaker the correlation. When looking at the variability in intensity measure amplitudes over the field, current approaches account for the point-to-point correlations between the grid points in each cell, but do not also account for the additional variability that arises over a cell. This additional variability can be computed using Eq. 8.2, which makes use of an effective correlation, ρeff, for the cell.

$$\Delta \phi \left( {\bf x} \right) \approx \phi \left( {\bf x} \right)\sqrt{1 - \rho_{\text{eff}}^{2} }$$
(8.2)

In Eq. 8.2, \(\phi \left( {\bf x} \right)\) is the within-event standard deviation of motions at the grid point for the cell.

To compute the effective correlation, consider the generic geometry shown in Fig. 8.2. The cell has an area of ∆x∆y and the grid point is indicated by the black dot. In this schematic we use a rectangular cell and locate the grid point in the geometric centroid, but there is no requirement to do this generally.

Fig. 8.2
figure 2

Geometry of spatial cells for computation of within-cell correlation adjustments

Full size image

The effective correlation is then computed as the expected value of the correlation for all possible spatial combinations of locations over the cell, as shown in Eq. 8.3.

$$\rho_{\text{eff}} \left( {T_{1} ,T_{2} } \right) = \frac{1}{\Delta x^{2} \Delta y^{2} }{\iiiint {\rho \left( {\left\{ {T_{1}, {\bf x}_{1} } \right\},\left\{ {T_{2}, {\bf x}_{2} } \right\}} \right)dx_{1} dx_{2} dy_{1} dy_{2} } }$$
(8.3)

Note that the default approach in traditional studies is to effectively assume perfect correlation of ρ = 1 for the motions over the cell, while the expression in Eq. 8.3 will always be less than unity for any finite cell size. Importantly, for the exponential spatial correlation models that are normally used, the larger the cell size, the smaller the effective correlation.

An important corollary of Eq. 8.3 is that inter-period correlations, that are used to represent correlations among building classes, need to be reduced from their commonly adopted values. Note that when multiple response periods are used as inputs for a fragility function for the same building class, no modification is required as in this case the multiple periods represent multiple attributes of the building at a single location. However, when single spectral ordinates represent different building types, and the exact locations of these buildings are unknown within the cell, we have to reflect the fact that there are many possible combinations of relative locations within the cell that would be associated with different correlation values.

Figure 8.3 demonstrates how the inter-period correlation values of Baker and Jayaram (2008) are modified to account for spatial cell size in a regular square grid of dimension ∆x = ∆y. One can appreciate that significant reductions in the correlations arise as the nominal cell size increases, i.e., as the spatial resolution decreases.

Fig. 8.3
figure 3

Impact of spatial discretisation size upon the effective inter-period correlations of response spectral ordinates. The upper panel shows conditioning upon a period of 0.1 s, while the lower panel shows conditioning upon a period of 1.0 s

Full size image

The next case to consider is the situation where we are interested in the correlations between potentially different intensity measures in different spatial cells. The relevant geometry in this case is shown in Fig. 8.4.

Fig. 8.4
figure 4

Geometry of spatial cells for computation of between-cell correlations

Full size image

Now the effective correlation is defined by Eq. 8.4, in which the cell sizes are assumed equal for both cells with dimensions Dx × Dy and the relative positions are defined by ∆x and ∆y. As before, the sizes of each cell can easily be different, the key concept is that we integrate to ensure that all possible combinations of spatial locations between cells are considered. The + = ∆x, ∆y specification on the integral limits is simply shorthand to denote the relative shift in the x2 and y2 co-ordinates relative to x1 and y1.

$$\rho_{\text{eff}} \left( {T_{1} ,T_{2} } \right) = \frac{1}{{D_{x}^{{^{2} }} D_{y}^{{^{2} }} }} \iiiint_{+=\Delta x\Delta y} {\rho \left( {\left\{ { {\bf x}_{1}, {\bf y}_{1} } \right\}, \left\{ { {\bf x}_{2}, {\bf y}_{2} } \right\},T_{1} ,T_{2} } \right)dx_{1} dx_{2} dy_{1} dy_{2} }$$
(8.4)

Figure 8.5 shows the impact of Eq. 8.4 when applied to a regular grid with relative cell offsets equal to integer multiples of the cell dimensions, i.e., ∆x = iDx for i ∈ \(\mathbb {Z}\), and similar in the y-direction. Again, the impact of the spatial discretisation increases as the resolution decreases.

Fig. 8.5
figure 5

Effective between-cell correlations, accounting for spatial discretisation. θ = 0 indicates that the cells all have the same y co-ordinates and we consider relative positions in the x-direction

Full size image

Note that the importance of considering these spatially discrete effects is that it allows one to work at a lower spatial resolution whilst still reflecting the appropriate levels of variability being input into fragility functions. In all of the cases considered in this section, as the cell size tends to zero we recover the expressions for the point-to-point cases (and continuous ground-motion fields).

3 Impact of the Ergodic Assumption upon Correlation Models

As previously mentioned, an ergodic dataset will make use of data from many different spatial locations and ground-motion models derived from this data therefore contain a degree of site-to-site variability that will not exist at a given site location. Correlation models that have been developed in the literature have, for the most part, been computed using a simple partitioning of ground-motion variability into just between-event, δB, and within-event, δW, components, as shown in Eq. 8.5.

$$\ln im\left( {\bf x} \right) = \mu \left( { {\bf x}; rup} \right) + \delta_{B} + \delta_{W} \left( {\bf x} \right)$$
(8.5)

Here, µ(x; rup) is the mean logarithmic intensity measure at site x for rupture scenario rup, and we indicate that δB and δW(x) are independent, and dependent of position, respectively.

Contrast this with a model in which systematic site effects, δS2S(x), are also considered. Now, the event-and-site corrected within-event residuals are represented by \(\delta_{W_{es}}\left({\bf x}\right)\), as shown in Eq. 8.6.

$$\ln im\left( {\bf x} \right) = \mu \left( {{\bf x};rup} \right) + \delta_{B} + \delta_{S2S} \left( {\bf x} \right) + \delta_{W_{es}}\left({\bf x}\right)$$
(8.6)

Between-event residuals are perfectly correlated (ignoring any parameterisation of nonlinear site effects) for all observations from a given event, so we focus upon the remaining within event correlations.

4 Correlations Between Spectral Ordinates at a Point

When deriving correlation models from ergodic datasets, the general expression for the within-event inter-period correlation is given by:

$$\rho \left( {T_{i} ,T_{j} } \right) = \frac{{{\rho_{S2S} \left( {T_{i} ,T_{j} } \right)\phi_{S2S} \left( {T_{i} } \right)\phi_{S2S} \left( {T_{j} } \right) + \rho_{SS} \left( {T_{i} ,T_{j} } \right)\phi_{SS}\left( {T_{i} } \right) \phi_{SS} \left( {T_{j} } \right)}}}{{\phi \left( {T_{i} } \right)\phi \left( {T_{j} } \right)}}$$
(8.7)

where ϕS2S(T) is the between site variability at period T, and ϕSS(T) is the single-station variability at period T. Almost all published correlation models are based upon this framework, with only a couple of exceptions (Kotha et al. 2017; Stafford 2017).

As shown in Stafford (2017), the ρS2S terms are relatively strong and represent different resonance and impedance effects that arise from sites with the same VS,30 values. Under a non-ergodic framework in which these systematic site effects are accounted for, the overall correlation changes from ρ → ρSS, and to weaker levels of correlation. However, this then requires that the spatial variations of the systematic site terms are evaluated. Currently this is very rare, but at least one regional risk model (Bommer et al. 2017) has attempted this and future applications are sure to move in this direction.

Note that when systematic site effects are accounted for, all of the expressions of the previous section related to spatial discretisation operate on these reduced correlation values. Therefore, we have compounded effects of weaker correlations and discretisation effects. At the same time we have systematic deviations from ergodic median predictions that reflect the systematic site response. Ultimately, what is happening is that we are transferring apparent aleatory variability out of the ergodic ground-motion model and into epistemic uncertainty within a partially non-ergodic model.

4.1 Spatial Correlations Between Spectral Ordinates

Turning now to the case where spatial correlations are considered, Eq. 8.8 shows the general expression to define the correlation from correlated random variables δS2S(x) and \(\delta_{W_{es}}\left({\bf x}\right)\) at two spatial locations.

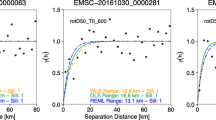
$$\rho \left( {{\bf x}_{i}, {\bf x}_{j} } \right) = \frac{{\rho_{S2S} \left( {{\bf x}_{i}, {\bf x}_{j} } \right)\phi_{S2S} \left( {{\bf x}_{i} } \right)\phi_{S2S} \left( {{\bf x}_{j} } \right) + \rho_{SS} \left( {{\bf x}_{i} ,{\bf x}_{j} } \right)\phi_{SS} \left( {{\bf x}_{i} } \right) \phi_{SS} \left( {{\bf x}_{j} } \right)}}{{\phi \left( {{\bf x}_{i} } \right)\phi \left( {{\bf x}_{j} } \right)}}$$
(8.8)

As with models for inter-period correlations at a point, spatial correlation models like Jayaram and Baker (2009) work on within-event residuals according to Eq. 8.5. These models generally use exponential correlation models to represent this spatial variability. In the case of Jayaram and Baker (2009), the authors find that the correlation length depends upon characteristics of the site conditions, namely, whether site conditions are clustered or not. These correlation lengths are shown in Fig. 8.6.

Fig. 8.6
figure 6

Correlation lengths within the Jayaram Baker (2009) spatial correlation model

Full size image

From the framework of Eq. 8.8, it can be appreciated what effect they are really observing. Let the separation distance between two sites be defined as ∆ = ||xi − xj||, and assume that exponential correlation models hold for both components of the within-event residuals:

$$\rho_{S2S} \left( {{\bf x}_{i} , {\bf x}_{j} } \right) = \exp \left[ { - \frac{\Delta }{{r_{S} }}} \right]\,\,\,\text{and}\,\,\,\rho_{SS} \left( {{\bf x}_{i} ,{\bf x}_{j} } \right) = \exp \left[ { - \frac{\Delta }{{r_{W} }}} \right]$$
(8.9)

The overall correlation can then be expressed as:

$$\rho \left( \Delta \right) = \frac{{{\phi_{S2S} \left( {{\bf x}_{i} } \right)\phi_{S2S} \left( {{\bf x}_{j} } \right)\exp \left( { - \frac{\Delta }{{r_{S} }}} \right) + \phi_{SS} \left( {{\bf x}_{i} } \right)\phi_{SS} \left( {{\bf x}_{j} } \right)\exp \left( { - \frac{\Delta }{{r_{W} }}} \right)}}}{{\phi \left( {{\bf x}_{i} } \right)\phi \left( {{\bf x}_{j} } \right)}}$$
(8.10)

Consider limiting cases in which we have full correlation of the systematic site effects rS  → ∞ (ρS2S →  1), and the case in which we have no correlation at all among the site effects rS  →  0 (ρS2S  →  0). In the first case, for rS  → ∞ we have:

$$\rho \left( {\Delta ;r_{S} \to \infty } \right) = \frac{{\phi_{S2S} \left( {{\bf x}_{i} } \right)\phi_{S2S} \left( {{\bf x}_{j} } \right) + \phi_{SS} \left( {{\bf x}_{i} } \right)\phi_{SS} \left( {{\bf x}_{j} } \right)\exp \left( { - \frac{\Delta }{{r_{W} }}} \right)}}{{\phi \left( {{\bf x}_{i} } \right)\phi \left( {{\bf x}_{j} } \right)}}$$
(8.11)

In the second case, for rS  →  0 we have:

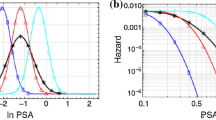
$$\rho \left( {\Delta ;r_{S} \to 0} \right) = \frac{{\phi_{SS} \left( {{\bf x}_{i} } \right)\phi_{SS} \left( {{\bf x}_{j} } \right)\exp \left( { - \frac{\Delta }{{r_{W} }}} \right)}}{{\phi \left( {{\bf x}_{i} } \right)\phi \left( {{\bf x}_{j} } \right)}}$$
(8.12)

The effects of these different conditions, as well as the case where rS =  rW (equivalent to not decomposing within-event residuals for systematic site effects) are shown in Fig. 8.7. For rS → ∞ we see that even for very large separation distances we will never tend to zero correlation because we will always have ρ ≈ ϕ2S2S/ϕ2. Conversely, for rS → 0 we have a nugget effect as when ∆ → 0 we have ρ ≈ ϕ2SS/ϕ2. Some studies, such as Stafford et al. (2019), have observed evidence for such nugget effects, but the authors at the time did not fully appreciate the origin of these effects.

Fig. 8.7
figure 7

Impact of spatial correlation of systematic site response upon overall spatial correlations

Full size image

As ergodic datasets have different degrees of inherent clustering and hence implicit rS values, the spatial correlations across site zones can vary significantly (Stafford et al. 2019). When modelling systematic site effects, the above effects need to be taken into account. This point applies both to the derivation of the models in the first instance (taking into account the systematic site terms), as well as during application where the differences in correlations among site zones should be accounted for. Note that for risk analyses working with site zonation models, the spatial correlation between cells of the systematic site effects should be close to zero (if not actually zero), if the two cells are not in the same zone.

5 Non-ergodic Risk Analyses for Seismic Sequences

The final contribution of the present chapter is to discuss issues of non-ergodic ground-motion models relevant for aftershock risk assessments. Studies such as Kuehn et al. (2016); Lee et al. (2020) have shown that systematic source effects from different events can be spatially correlated. However, ergodic datasets rarely have large numbers of events at close spatial locations and so the between-event variability of published models is greater than what should be expected within a single small spatial region. In addition to this, studies (e.g., Kanamori et al. 1993) have discussed the effects that time has upon healing faults and changing frictional characteristics. Therefore, during aftershock sequences, particularly when events are re-rupturing portions of a previously ruptured surface, the frictional characteristics of the rupture surfaces may have less variability than in an ergodic database.

A reasonable working hypothesis is therefore that between-event variability in a small spatial region is lower than the published ergodic values, and that aftershock sequences may have even lower between event variability again. This is important because within a Bayesian updating framework (Stafford 2019) it is possible to actively refine existing ground-motion models as new data becomes available. As a result, aftershock risk analyses can adapt during the sequence to improve risk assessments associated with a given sequence.

To investigate whether we see empirical evidence for this hypothesis, the New Zealand strong ground-motion database is analysed here. On the left of Fig. 8.8, all of the crustal events for which strong-motion records are available are shown. A declustering algorithm (Gardner and Knopoff 1974) is then applied to this data and the two largest clusters of events are extracted. These two clusters correspond the Canterbury and Marlborough sequences and are shown on the right of Fig. 8.8.

Fig. 8.8
figure 8

Shallow crustal earthquakes in New Zealand (left), and two key clusters (right) in the Canterbury (red) and Marlborough (green) sequences

Full size image

A closer view of the spatio-temporal evolution of these earthquake sequences is provided in Fig. 8.9.

Fig. 8.9
figure 9

Spatio-temporal evolution of the Canterbury (left) and Marlborough (right) earthquake sequences. Marker size indicates magnitude, while marker shade shows the passage of time from dark being the oldest to light being the most recent

Full size image

For the total database of all crustal events, the NGA-West2 model of Chiou and Youngs (2014) was used to define total residuals that were then partitioned via a mixed effects regression analysis to obtain variance components. The betweenevent residuals for the events in the Canterbury and Marlborough clusters were then extracted and their distribution was compared to the overall between-event variability for the entire database.

Figure 8.10 shows the temporal evolution of the event terms for the Canterbury sequence at two different response periods. The horizontal dashed lines show the total between-event variability for the entire database considered, while the blue lines show loess fits to the data. The shaded region shows the prediction interval for this local fit and it is very clear that this band is significantly narrower than the overall between-event variability.

Fig. 8.10
figure 10

Temporal evolution of event terms within the Canterbury earthquake sequence. The upper panel shows event terms for T = 0.01 s, while the lower panel corresponds to T = 1.0 s. Markers are sized according to magnitude. Horizontal dashed lines show the ergodic between-event standard deviation for the total database considered. The blue line is a local moving average fit to the event terms and the grey band shows the prediction interval for this curve

Full size image

However, Fig. 8.10 also shows that event terms within the sequence can fluctuate to span a significant portion of the overall ergodic variability.

Similar results can be seen in Fig. 8.11 for the Marlborough sequence. However, in this case we see less temporal fluctuation and a more consistent offset at negative between-event residuals. Of course, just two sequences have been investigated here, but it is important to point out that they have not been identified on the basis of them having any particular characteristics. They are simply the two largest clusters that could be extracted from the available New Zealand strong-motion database. In that sense, the results presented here can be thought of in a similar vein to a blind prediction. That is, a hypothesis was formulated via a thought experiment, and the results obtained are entirely consistent with expectations from that experiment.

Fig. 8.11
figure 11

Temporal evolution of event terms within the Marlborough earthquake sequence. The upper panel shows event terms for T = 0.01 s, while the lower panel corresponds to T = 1.0 s. Markers are sized according to magnitude. Horizontal dashed lines show the ergodic between-event standard deviation for the total database considered. The blue line is a local moving average fit to the event terms and the grey band shows the prediction interval for this curve

Full size image

In Figs. 8.10 and 8.11, just two periods are shown, but additional summarising results are presented in Fig. 8.12. In Fig. 8.12, the standard deviation of the event terms in the Canterbury and Marlborough sequences are compared to the between-event variability computed from a mixed effects regression analysis using all of the New Zealand crustal data. The standard deviations for the individual sequences are computed from event terms extracted from the same analysis used to define the overall variability for the entire database.

Fig. 8.12
figure 12

Variation of the between-event standard deviation against period. Blue markers show the variability computed from all New Zealand crustal events from a mixed effects analysis. Red markers show the standard deviation of the event terms in the Canterbury sequence, while green markers correspond to the Marlborough sequence

Full size image

The results in Fig. 8.12 show a significant reduction at short periods, but it must also be appreciated that it is a significant reduction from a very large level of between event variability for this database. That said, the values for the Canterbury sequence hover around the 0.3 level in natural logarithmic units and this is smaller than typical ergodic values.Footnote 2

It is also important to highlight that these sequences also contain many, many more events than those shown here. Those additional events did not have their strong-motion data processed as part of the New Zealand database analysed here, but in principle a significantly greater amount of data could be available, albeit from small magnitude events, to help constrain the properties of the sequence. Under the assumption that the event terms from the smaller events correlate with those of the larger events, the addition of this weaker motion data could significantly improve one’s ability of constrain features of the particular sequence.

This includes overall regional and sequence-specific offsets from ergodic models, as well as systematic site effects. Correlations among these systematic effects, as well as residual correlations can also be updated during the sequence. Within the Bayesian updating framework presented by Stafford (2019), these characteristics can be progressively updated as events occur such that systematic terms become more constrained during the sequence.

Naturally, further work is required to analyse many more sequences to test whether the evidence presented here persists more generally. However, it is clear that some features of these findings, particular the reduction of between-event variability arising from spatially correlated source effects will prove to be a more general finding.

6 Conclusions

Regional and portfolio risk analyses have traditionally made use of groundmotion model components that have primarily been derived for use in hazard applications. There are attributes of these components that are not ideally suited for use within risk analyses and this chapter has highlighted some of these issues. In particular, the increasing use of partially non-ergodic approaches within ground-motion modelling has implications for how covariances among intensity measures are represented. The vast majority, if not all, risk analyses currently conducted do not properly account for these effects when attempting to move towards partially non-ergodic approaches. The chapter has shown pathways to address these issues and has also introduced evidence to suggest that withinsequence between-event variability may be over-estimated. This latter point has implications for aftershock risk analyses. However, the potential benefits of working with a reduced variability may be offset by epistemic uncertainty for the earliest events in the sequence.